😀

DeepGo: Predictive Directed Greybox Fuzzing

作者

传统方法

传统的定向模糊测试的适应度指标优化主要基于启发式算法，这种算法通常依赖于历史执行信息，对尚未执行的路径缺乏预见性。因此，那些具有复杂约束的难以执行的路径将阻碍DGF达到目标，使DGF效率降低。

例如，当使用到目标的基本块级距离作为适应度度量时，没有考虑路径可行性，优先考虑距离较短的种子，因此，那些难以执行且约束复杂的路径会阻碍DGF到达目标位点，从而降低DGF的效率

作者方法

提出了路径转换模型，该模型将DGF建模为通过特定路径转换序列到达目标位点的过程。突变产生的新种子会引起路径转移，高回报路径转移序列对应的路径表明通过它到达目标位点的可能性很大。
为了确定最优路径，我们开发了一种用于模糊测试的强化学习(RLF)模型来生成具有最高序列奖励的过渡序列。RLF模型可以结合历史路径转换和预测路径转换生成最优路径转换序列，并结合策略指导模糊测试的突变策略
为了实现高回报路径转换序列，我们提出了行动组的概念，该概念综合优化模糊测试的关键步骤，以实现最优路径，从而有效地达到目标。

路径转换模型

路径转换模型中的元素

路径。每个路径对应于模糊器种子队列中的一个种子。我们使用AFL中的trace_bits来记录路径中被覆盖的分支和分支的命中次数，从而区分不同的路径
行为。fuzzer的行为意味着在特定的位置使种子发生变异。我们关注的是发生突变的位置(即字节)，而不是它使用的mutator。模糊器采取一系列动作，逐渐到达目标地点。
路径转换。如果新输入的执行路径与种子的执行路径不同，则种子上的突变将导致路径转换。如果新输入的路径与种子的路径相同，则突变导致自路径转换。
奖励。路径转换的奖励表示由路径转换引起的种子价值的变化。
策略。策略是fuzzer在每个路径中选择动作的策略，表示为与动作对应的概率列表。在该策略下，模糊器会选择不同概率的动作。

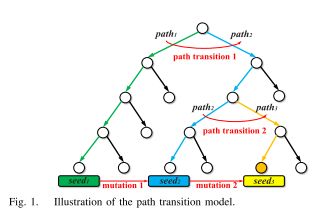
图1为示例程序的执行树，其中节点表示基本块，边表示基本块过渡。标记为绿色的执行路径path1被种子s1覆盖，标记为蓝色的执行路径path2被种子s2覆盖，标记为黄色的执行路径path3被种子s3覆盖。标记为橙色的节点为目标基本块，path3为到达目标站点的最优路径。

在模糊测试过程中，首先，模糊器采取行动使种子s1发生突变，产生新的种子s2，使路径1转移到路径2。然后，模糊器采取行动使种子s2发生突变，使路径2转移到路径3并到达目标位点。通过两次路径转换，模糊器生成到达目标的最优路径path3，由路径转换序列(path transition 1，path transition 2)表示。

模糊器对突变种子采取不同的行动会导致不同的路径转移，我们使用奖励来量化路径转移的有效性，并使用期望序列奖励来量化行动的有效性。

路径转换和动作的量化

使用种子值来评估不同的路径，基于它们对模糊器到达目标地点的贡献。种子值是根据路径对应的种子的四个特征来计算的

种子到目标的距离: 在DGF中，种子距离越短，模糊器满足的路径约束越少，就能到达目标点
满足分支条件的难易程度: 难度越低，模糊器更容易满足到达目标点的路径约束
执行速度: 在种子执行过程中，模糊器可能会陷入循环(例如while和for循环)，这降低了执行速度，并且不利于模糊器到达目标站点。因此，为了提高模糊测试效率，我们更倾向于选择执行速度更快的种子
种子是否“被偏爱”: 我们更喜欢标记为“偏爱”的种子，因为这些种子可以覆盖所有已探索的分支。通过模糊测试偏爱的种子，我们可以对所有探索的分支进行分支反演，以覆盖通向目标位点的新分支

使用熵权法根据四个因素的信息熵来确定它们的权重。信息熵值越小，则因子权重越小，表明该因子对种子价值的整体评价影响较小

$V^s(p_t)=W_1*d_s+W_2*ED_s+W_3*E_{x_s}+W_4*F_{v_s}$

$V^s(p_t)$ 表示路径 $p_t$ 的种子值
$W_1$ 、 $W_2$ 、 $W_3$ 、 $W_4$ 为权重
$d_s$ 表示距离
$E_{x_s}$ 表示执行速度
$F_{v_s}$ 表示在哪个位置更有利
每个元素的熵: $E_j=-\frac{1}{\ln{n}}\sum^n_{i=1}\frac{p_{ij}}{\ln(p_{ij})}$
每个元素的权重: $W_j=\frac{1-E_j}{n-\sum^{n}_{j=1}E_j}$
每个元素权重的标准化: $W_j'=\frac{W_j}{\sum^n_{j=1}w_j}$

根据种子值计算奖励来评估路径转换的有效性

$r(p_t,a_t,p_{t+1})=V^s(p_t+1)-V^s(p_t)$

$r(p_t,a_t,p_{t+1})$ 表示奖励
$a_t$ 表示从路径 $p_t$ 转换到 $p_{t+1}$ 采取的行动
$V^s(p_t+1)$ 、 $V^s(p_t)$ 表示两个路径的种子值

Q1: 如何量化分支条件的难易程度?

作者用分支概率来衡量满足分支反演的难易程度，这是基于分支命中的统计。在静态分析期间，我们首先获得了每个分支的兄弟分支的信息。如果被覆盖的分支的兄弟分支仍然是未覆盖的(即，未探索的分支)，满足覆盖未探索分支的分支反转将允许模糊器从覆盖的路径转移到新的路径。然后，我们计算分支命中数来计算未探索分支的分支概率。如果模糊器总是命中输入发生突变的覆盖分支，而不能命中未探测分支，则表明模糊器难以满足分支反演。最后，我们用分支概率来量化满足分支反演的难度

$P(ubr)=\frac{1}{\sum_{br\in \phi(cond)}hit_{br}+1}$

其中 $ubr$ 表示为未探索的分支，通过检查被覆盖的分支的兄弟姐妹是否被覆盖以找到未探索的分支

$\phi(cond)$ 表示在相同条件下能够覆盖到的分支的集合

$hit_{br}$ 表示在Fuzz中记录的分支命中数

$ED_s=\frac{\sum_{br\in\phi(s)}P(br)}{|\phi(s)|}$

$s$ 表示种子

$ED_s$ 表示难度

$\phi(s)$ 表示种子路径种所有未探索分支的集合

Q2: 什么叫“branch inversion”

就是路径转换

Q3: “ $hit_{br}$ 表示在Fuzz中记录的分支命中数” 命中什么分支?

同一条件下覆盖分支的命中数

预期序列奖励

在路径转换模型中，根据策略选择的动作导致的路径转换会影响后续的路径转换序列，从而影响到达目标站点。为了评估路径转换对到达目标地点的贡献，我们将期望序列奖励定义为模糊器按照一定策略生成的路径转换序列的期望奖励之和。它可以用Bellman方程递归地计算

$Q_\pi(p,a)=E_{p'\sim p}[r(p,a,p')+\gamma v^t_\pi(p')]$

$p'\sim p$ : 表示从路径 $p$ 转移到路径 $p'$ 的概率
$\gamma$ : 表示折现因子
$r(p,a,p')$ : 表示路径转移的奖励
$v^t_\pi(p')$ : 表示路径 $p'$ 的转移值

$\begin{equation}v^t_\pi(p')=\left\{ \begin{aligned} 0 ,\quad if\quad p=p_{ter}\\ \sum_a\pi(a|p)*Q_\pi(p',a), \quad others\\ \end{aligned}\right.\end{equation}$

$p_{ter}$ :表示最终路径，即无论在这条路径上采取什么动作只能引起自转移
$\pi$ : 表示选择动作的策略(AFL中为随机策略)
$\pi(a|p)$ : 表示使用策略 $\pi$ 在分支 $p$ 上采用动作 $a$ 的概率

Q4: 什么是Bellman方程

总体架构

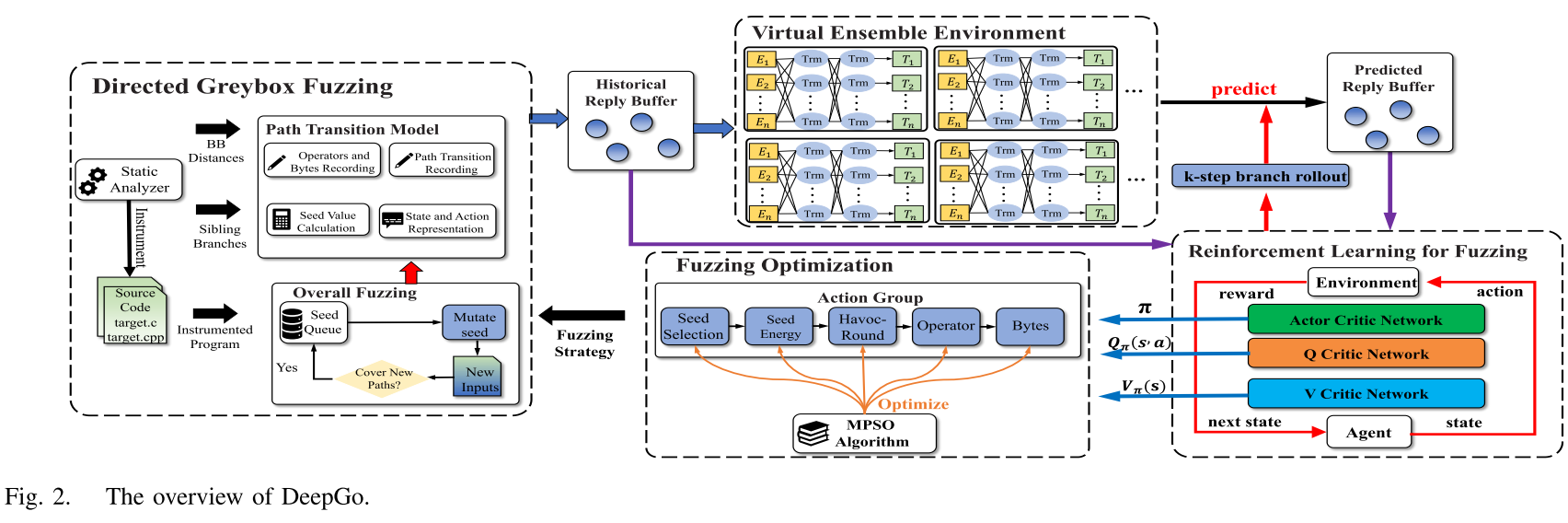
DeepGo使用深度神经网络来预测潜在的路径转换和相应的奖励
利用强化学习将历史路径转换与预测路径转换相结合，得到具有相应策略的最优路径转换序列
基于动作组，对模糊测试策略进行综合优化，得到最优路径转换序列

将DeepGo的模糊测试过程划分为不同的模糊测试周期，每个周期持续大约20分钟。在每个模糊测试周期中，DeepGo需要执行四项任务，包括

使用模糊器测试程序并提供历史路径转换以训练VEE和RLF模型
VEE提供预测路径转换以训练RLF模型
RLF为FO组件提供转换值、预期序列奖励和策略
FO分量利用MPSO算法对动作组进行优化，并向DGF提供模糊测试的优化策略

Q5: 什么是MPSO算法

Directed Greybox Fuzzing Component

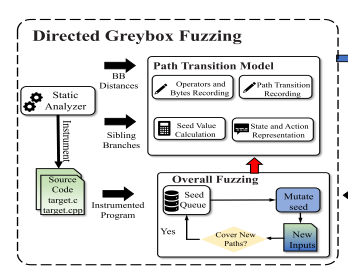
DGF组件不断使种子突变，以产生到达目标位点的输入。该组件包含一个静态分析器和一个模糊器。在编译时，静态分析器计算基本块级距离(BB距离)，记录每个分支的兄弟分支，并插桩目标程序。一旦模糊测试活动启动，模糊测试器就会不断变异种子来测试程序。值得注意的是，路径转换模型被合并到DGF组件中。

Virtual Ensemble Environment

VEE用于预测潜在的路径转换和相应的奖励。VEE由dnn组成，并与强化学习模糊测试组件共享历史重放缓冲区和预测回复缓冲区。历史重放缓冲区和预测回复缓冲区都是存储四元组的数据缓冲区，即 $(path,action,next\_path,reward)$ 。给定一个元组 $(path, action)$ ，训练后的VEE将根据不同路径转换的概率，预测该动作的下一个路径和奖励，表示为 $(next\_path, reward)$ 。

模糊器不能在有限的时间预算(例如，24小时)内采取所有路径上的所有行动。为了预测尚未采取的行动所引起的潜在路径转移和奖励，我们设计了VEE来模拟路径转移模型，并预测潜在路径转移和相应的奖励。

Input and Output Encoding

在训练VEE之前，我们要对路径、动作、奖励进行编码。我们设计VEE的编码方法有两个目的。首先，VEE基于已探索路径中记录的路径转换来预测新路径的潜在路径转换。其次，为了提高VEE的训练效率，我们需要使用低维向量来表示路径和动作。例如，将trace_bits映射到65536维的向量来表示路径将显著降低dnn的训练速度。因此，在确保能够清楚区分不同路径和行动的同时，我们尝试使用低维向量来表示路径、行动和奖励。

Path: 应用耦合数据嵌入(CDE)算法将AFL中的路径(用trace_bit表示)编码为20维连续向量，并对每个维度的值进行归一化。CDE用于将离散向量表示为连续向量，同时保留区分路径的主要特征。根据CDE方法，一个20维向量既可以区分不同路径的主要特征，又可以降低路径的维数，从而提高dnn的训练效率。如果trace_bits表示的两条路径越相似，对应的20维向量之间的欧几里得距离就越近。

Q6: 什么是CDE算法

**Action: **根据突变位置对动作进行编码。以图1为例，种子s1代表一个100字节的种子，如果模糊器选择s1的第4个字节作为突变位置，无论选择哪个突变体，模糊器都会从第4个字节开始对s1进行突变，该动作的编码为4/100=0.04。所有动作的值也被规范化。

**Reward: ** $r(p_t,a_t,p_{t+1})=V^s(p_t+1)-V^s(p_t)$

Tranning of VEE

VEE能够基于历史模糊测试信息预测潜在路径转换的概率和奖励。VEE使用四元组进行训练，即 $(path,action,next\_path,reward)$ ，其中 $action$ 代表可能发生突变的种子字节，而不是具体的突变。因此，对于不同的突变体，相同的动作会导致不同概率的路径转换。

VEE通过分析一个字节上突变的历史信息，可以预测由于采取这个动作而引起的路径转换，即用不同的突变子对这个字节进行突变。对于已经发生突变的字节，我们使用VEE来预测由于使用不同的突变器对字节进行突变而导致的不同路径转换的概率和奖励。对于尚未突变的种子或字节，我们使用具有相似结构的种子或具有相似偏移量的字节来预测突变行为引起的路径转换的概率和奖励。

基于CDE编码方法测量相似度。如果表示两种种子的20维向量的欧氏距离较短，则说明这两种种子更相似。此外，在一个种子中，两个动作的类似编码值表示相应字节的类似偏移量。

我们利用深度神经网络构造VEE来模拟路径转移模型中的路径转移行为。形式上，让 $f:(path, action)\rightarrow(next\_path, reward)$ 表示以元组 $(path, action)$ 作为输入并输出元组 $(next path, reward)$ 的dnn。我们用 $\theta$ 表示DNN的可训练权参数，用一组训练样本(X, Y)训练DNN，其中X表示一组输入，Y表示相应的输出。在路径转移模型中，由于同一路径上的相同动作可能导致不同概率的不同路径转移，因此路径转移模型本质上是一个概率模型。因此，在设计DNN $f:(path, action)\rightarrow(next\_path, reward)$ 和损失函数时，我们主要解决VEE的任意不确定性和认知不确定性，以提高其预测精度。

**任意不确定性: ** 任意不确定性产生于模糊测试中路径转换的不可预测性。例如，对相同的突变位置使用不同的突变子可能会导致不同的路径转换。为了捕捉任意的不确定性，我们使用下一个路径和奖励的高斯概率分布来预测不同路径转换的概率和相应的奖励，这些奖励可能是由路径 $p_t$ 中采取的行动 $a_t$ 引起的。我们使用可训练的权重参数来表示下一个路径 $p_{t+1}$ 的高斯概率分布，奖励 $r_t$ 可以是根据输入元组 $(p_t, a_t)$ 表示

$P(p_{t+1},r_t|p_t,a_t,\theta)=N(\mu_\theta(p_t,a_t),\sum_\theta(p_t,a_t))$

其中 $N$ 表示高斯分布的均值， $\sum_\theta$ 来表示方差，他表示均值的不确定性

DNN的输出和训练集中的真值标签 $y\in Y$ 之间的损失函数为

$L(\theta)=\sum^N_{n=1}[\mu_\theta(s_n,a_n)-s_{n+1}]^T\sum^{-1}_\theta(s_n,a_n)[\mu_\theta(s_n,a_n)-s_{n+1}]+\log \det \sum_\theta(s_n,a_n)$

认知不确定性: 认知的不确定性来自于大多数深度神经网络采用的随机抽样方法。由于单个DNN无法对所有训练数据进行采样，因此可能存在DNN存在认知缺陷且无法准确预测输出的区域。为了捕获认知不确定性，我们采用轨迹采样概率集成算法(PETS)将所有dnn聚合到一个虚拟集成环境中。我们使用相同的随机抽样方法，通过从历史回放缓冲区中采样四元组来训练dnn。所有dnn生成的预测输出由高斯概率分布表示，并对其结果进行加权以产生最终预测。

$P(p_{t+1},r_t|p_t,a_t,\theta)=\frac{1}{n}\sum^n_{i=1}P(p_{t+1},r_t|p_t,a_t,\theta_i)$

$n$ 为DNN个数，考虑到训练速度、GPU内存限制和VEE的预测精度，我们使用6个相同的dnn构建VEE，并采用6个dnn概率的平均值作为模型预测。通过对所有深度神经网络进行加权平均，可以减轻单个深度神经网络在特定区域的随机抽样所带来的认知缺陷。

Q7: PETS算法?

Determine the path transition from the preducted distribution

给定一个输入 $(p_t, a_t)$ ， DNNs以高斯概率分布输出潜在路径转移和相应的奖励，表示为 $(p_{t+1}, r_t)$ 。然而，在DGF中，突变种子只会导致特定的路径转变。因此，我们采用随机抽样的方法，根据不同路径转换的预测概率来确定下一个路径 $p_{t+1}$ 。

Reinforcement Learning for Fuzzing Model

该模型利用强化学习模型，将历史路径转换和预测路径转换结合起来，学习使序列奖励最大化的策略。RLF模型由Actor网络、Q-Critic网络和V-Critic网络组成。经过训练，Q-Critic网络可以评估每个动作引起的期望序列奖励 $Q_\pi(p, a)$ ， V-Critic网络可以评估每个路径的过渡值 $V^t_\pi(p)$ ， Actor网络可以学习策略 $\pi$ 以最大化序列奖励。

为了使模糊器更有效地转向目标位置，即通过高奖励路径转换序列，我们需要学习一种策略来选择动作以最大化序列奖励。由于路径转移模型中的路径、动作和路径转移数量巨大，很难使用传统的数学方法(如动态规划(DP)[3])来学习策略并计算期望的序列奖励。因此，我们开发了基于强化学习算法Soft Actor-Critic (SAC)[15]的模糊测试强化学习(RLF)模型。

Q8: SAC算法?

The Design of RLF model

按照SAC的结构，RLF模型由Actor网络、Q-Critic网络和V-Critic网络组成。在训练过程中，我们训练Q-Critic网络来评估期望序列奖励，训练V-Critic网络来评估每个路径的过渡值。利用期望序列奖励和转移值，训练Actor网络来优化策略，以增加选择具有高期望序列奖励的行为的概率。

Training data processing and collecting

我们将路径转换模型视为强化学习中的环境，并将路径转换模型中的模糊器、路径、动作、路径转换和奖励映射到强化学习中的智能体、状态、动作、状态转换和奖励。此外，RLF重用了VEE的路径、动作和奖励编码方法。由于我们将历史路径转换和预测路径转换结合起来训练RLF以赋予RLF模型前瞻性，因此我们以不同的方式收集历史路径转换和预测路径转换。

**收集历史路径转换: **由于DGF的环境不同于传统的强化学习过程，在传统的强化学习过程中，状态转换是连续生成的，并表示为 $(s_0,a_0, s_1, a_1, …，, a_{n−1},s_n)$ ， RLF的训练数据处理不同于传统的强化学习(如SAC)。在DGF中，模糊器可能会使一个种子多次突变，从而导致同一路径的不同路径转换。这意味着模糊器可能停留在某个路径上，并采取不同的动作来引起不同的路径转换。因此，RLF模型不可能在短时间内(例如几秒)通过计算序列奖励来获得完整的路径转换序列并评估当前策略的有效性。基于此考虑，在每个模糊测试周期中，模糊器根据策略选择动作以引起路径转换。历史路径转换存储在历史回复缓冲区中，并在模糊测试周期结束时由RLF模型加载，以便在下一个模糊测试周期中训练RLF。

**收集预测的路径转换: ** 使用VEE来模拟路径转换模型，并采用k步分支铺展策略来获得路径转换模型中尚未发生的预测路径转换。在k步分支rollout策略中，RLF模型被视为agent，它根据初始策略在每条路径上选择一系列动作引起k个路径转换，生成一个新的长度为k的路径转换序列。我们使用图3来说明k步分支展开策略的过程。假设 $(p_0,a_0,p_1, a_1, …,p_i,a_i,..., a_{n−1},p_n)$ 为路径转换模型中的历史路径转换序列。我们以 $\pi$ 为起点，使用RLF的策略 $\pi$ 来选择一系列动作 $a'_i, a '_{i+1},…,a ' _{i+k−1}$ 引起k个路径转换，生成一个新的k长度的路径转换序列 $(pi, a '_i, r_i, p ' _{i+1})， (p '_{i+1} , a ' _{i+1}, r ' _{i+1}, p '_{i+2})，…， (p ' _{i+k- 1} , a ' _{i+k - 1}, r '_ {i+k - 1}, p '_{ i+k})$ 。这里，k是一个超参数，它会影响VEE预测的准确性和RLF模型设计策略的预见性

在k步分支展开过程中，预测可能需要覆盖多个测试用例。在不同的测试用例中，由字节位置定义的相同动作可能是不对齐的(例如，由于不同的测试用例长度，一个测试用例中变异字节的位置可能与其他测试用例中的变异字节不对齐)。为了处理这种偏差，我们使用 $mutation\_ID∧(path\_ID >> 2)$ 来区分过程中产生的不同中间测试用例。例如，对于覆盖相同路径的testcase1和testcase2，我们仍然为它们分配不同的id，以便我们可以区分不同中间测试用例上的突变。这样，即使testcase1和testcase2的相同字节发生突变，我们也不认为这两个突变引起的路径转换的概率和奖励是相同的。

Training of the RLF model

RLF模型结合了历史路径转换和预测路径转换来训练Actor网络、Q-Critic网络和V-Critic网络。在DGF中，我们的目标是让模糊器采用具有高期望序列奖励的动作，同时探索不同的动作来产生新的路径转换。因此，在RLF中，我们使用熵来度量选择动作的随机性。假设我们根据策略 $\pi$ 选择状态 $s_t$ 下的动作，并且选择动作的概率服从 $\pi(·|s_t)$ 的分布，则动作的熵计算为

$H(\pi(·|s_t))=E_{a\sim \pi(·|s_t)}[-\log\pi(·|s_t)(a)]$

在RLF模型中，行动者网络的目标是学习一个使奖励和熵最大化的策略 $\pi^*$ 。

$\pi^*=\arg\max_\pi E_{(s_t,a_t)\sim \rho\pi}[\sum_t r(s_t,a_t,s_{t+1})+\alpha H(\pi(·|s_t))]$

其中 $r(s_t,a_t,s_{t+1})$ 为奖励 $H(\pi(·|s_t))$ 为熵 $\alpha$ 是在SAC算法中提出的平衡勘探和利用的系数。

然后，我们构建了Q-Critic网络的目标函数和V-Critic网络的目标函数来训练Q-Critic网络的参数 $\omega$ 和V-Critic网络的参数 $\phi$ 。

$J_{v^\pi}(\phi)=\frac{1}{2}(\gamma r_t+V^\pi_\phi(s_{t+1})-V^\pi_\phi(s_t))^2$

$J_{Q^\pi}(\omega)=(r_t+\gamma Q_\omega^\pi(s_{t+1},a_{t+1})-Q_\omega^\pi(s_t,a_t))^2$

对于Actor网络，我们训练Actor网络的参数 $\sigma$ 使动作的期望序列奖励最大化，从而使序列奖励最大化

$J_\pi(\sigma)=\max_\sigma Q(s_t,\pi_\sigma(·|s_t))$

通过最小化这三个目标函数，我们训练了这三个网络中的参数来计算期望的序列奖励和转移值，并设计了能够最大化序列奖励的行为选择策略。经过良好训练的RLF模型为FO组件提供了两种类型的优化信息:

估计的期望序列奖励和估计的过渡值
在每个路径上选择动作的策略

Optimize Fuzzing Strategies Based on Action Group

优化单一的模糊测试策略可能不会显著地引导模糊器走向最优路径转换序列。因此，我们提出了由五要素组成的行动组的概念，并尝试对多种模糊测试策略进行综合优化。此外，我们提出了多元素粒子群优化算法(MPSO)来同时优化行动群中的元素。

Q9: MPSO算法?

The concept of action group

我们将操作组定义为由五个元素组成的元组。

种子选择(SS): 表示一个种子被模糊器选中进行模糊处理的概率。

种子能量(SE): 表示分配给种子的能量，这决定了在变异阶段可以应用于种子的突变数量。

变异轮数(HR): 表示在变异阶段用于选择不同的突变器和字节的循环轮数。所有选定的突变和字节被集成到一个单一的破坏行动。取值为2、4、8、16、32、64、128。

突变子(MT): 表示选择使种子发生突变的突变子。与AFL[24]类似，DeepGo保留了16种不同类型的突变体。

位置(LC): 表示选择突变的种子的突变位置。

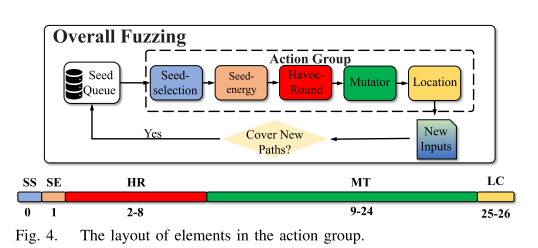
每个动作组表示为由5个元素组成的27维向量。如图4所示，SS和SE都是一维向量。SS的值表示在[0,1]范围内的概率。模糊器根据SS选择要模糊的种子，SE的值表示分配给种子的能量，模糊器根据SE计算种子的突变次数。HR是一个7维向量，其中每个维度表示选择7个不同的HR值(即2,4,8,16,32,64和128)之一的概率。该模糊器基于HR对变异阶段用于选择不同突变体和突变位置的循环次数进行采样。MT是一个16维向量，其中每个维表示从16种不同类型的突变体中选择一种的概率。LC是一个二维向量，第一维表示选择最优位置的概率，第二维表示选择常用位置的概率。

我们将种子的突变位置分为两类:最优位置和普通位置。最优位置包括RLF模型策略选择的概率大于80%的突变位置，而普通位置包括所有其他突变位置。在MT和LC的基础上，模糊器对突变体和突变位置的类型进行采样。模糊器不断改变种子，根据行动组中的五个要素产生新的输入。如图4所示，我们将每个元素表示为一个向量，并将五个向量连接成一个向量，以表示种子的动作组。

Multi-elements Particle Swarm Optimization algorithm

为了同时优化行动群中的五个元素，我们将每个行动群视为一个由27维向量表示的粒子，并将行动群的优化视为一个多元素优化问题。我们提出了一种多元素粒子群优化算法(MPSO)来实现优化。动作群的优化可以引导模糊器向具有高序列奖励的期望路径转换序列移动。

正如我们在第二节中所介绍的，粒子群算法使用无质量粒子来模拟鸟群中的鸟。每个粒子单独搜索最优解，并将其记录为局部最优值。然后在整个群中的粒子之间共享局部最优值，以找到全局最优值作为最优解。这些粒子有两个基本属性:速度和位置。速度表示运动的速度，位置表示运动的方向。群体中的所有粒子会根据整个群体共享的局部最优值和全局最优值不断调整自己的速度和位置:

$v_i=\omega*v_i+r*(lbest_i-x_i)+r*(gbest_i-x_i)$

$x_i=x_i+v_i$

其中 $v_i$ 为第 $i$ 个粒子的速度， $x_i$ 表示第 $x$ 哥粒子的位置， $r$ 表示在[0,1]范围内的随机位移权值, $lbest_i$ 表示第 $i$ 个粒子找到的全局最佳位置, 惯性因子 $\omega$ 是非负值，其值越大，粒子群算法的全局寻优能力越强，局部寻优能力越弱。在本文中，我们采用线性递减惯性权值(LDIW)方法将 $\omega$ 的值设置为

$\omega=\omega_{ini}-(\omega_{ini}-\omega_{end})*(g/G)$

$\omega_{ini}$ 表示初始惯性值, $w_{end}$ 表示最终惯性值。在LDIW中其值通常分别是0.4和0.9。 $g$ 表示当前粒子完成的迭代次数，等于模糊器对相应种子进行的突变次数。 $G$ 为最大迭代次数，等于根据种子能量计算的总突变次数。在DeepGo中，种子的突变时间由分配给种子的能量决定。

本地最佳位置和本地效率: 在MPSO算法中，每个粒子都有自己的局部最优位置 $lbest$ 和局部效率 $eff_{local}$ 。给定一个粒子，只有当粒子在 $x_1$ 处获得的局部效率大于 $x_2$ 处的局部效率时，才认为位置 $x_1$ 优于位置 $x_2$ 。我们用局部效率来量化由五个元素组成的模糊测试对一个特定粒子的突变效率。局部效率是根据模糊器在粒子对应路径上所有突变的平均期望序列奖励来计算的。在DGF中，种子上的每个突变都会导致路径从路径 $p$ 到路径 $p'$ 的转变。在一个路径转移中我们使用 $r+\gamma V^t_\pi(p')$ 来评估一个预期序列回报，基于此我们可以计算本地效率为

$eff_{local}=\frac{\sum^g_{i=1}r_i+\gamma V^t_\pi(p')}{g}$

其中 $V^t_\pi(p')$ 表示第 $i$ 个突变所覆盖的路径 $p '$ 的过渡值。

全局最佳位置和全局效率: 用全局效率来量化模糊器的模糊测试效率。由于模糊器的全局效率取决于不同粒子的局部效率和粒子之间的关系，因此我们根据模糊测试周期内的模糊测试效率来确定所有粒子的全局位置。只有当模糊器的模糊测试效率高于其他任何位置时，粒子当前才处于全局最佳位置(gbest)。我们使用模糊测试周期中的平均序列奖励来评估全局效率:

$eff_{global}=\frac{\sum^U_{j=1}\sum^{g_j}_{i=1}r_i+\gamma V^t_\pi(p'_j)}{\sum_{j=1}^Ug_j}$

其中 $eff_{global}$ 表示全局效率, $s_j$ 表示第j个种子， $g_j$ 表示种子 $s_j$ 的突变次数， $U$ 表示在当前模糊测试周期中被模糊化的种子数量

在模糊测试过程中，我们根据 $eff_{local}$ 和 $eff_{global}$ 计算粒子的局部效率和全局效率，并记录lbest和gbest。我们根据 $v_i$ 、 $x_i$ 和 $\omega$ 更新粒子的空间位置，将所有粒子向lbest和gbest方向移动。通过该方法，我们优化了所有种子的动作组，通过最优路径转换序列引导模糊器向目标移动。

Q10: 什么是MannWhitney U检测?

Q11: 什么是varga-delaney统计量?

目录