🤔

Better Pay Attention Whilst Fuzzing

作者

• Shunkai Zhu - 浙江大学 - 机器学习、模糊测试
• Jingyi Wang - 浙江大学 - 机器学习
• Jun Sun - 新加坡管理大学 - 模糊测试、智能合约、神经网络
• Jie Yang - 浙江大学 - 社交网络、机器学习
• Xingwei Lin - 蚂蚁集团 - 模糊测试、漏洞挖掘、LLM
• TianyiWang - 浙江大学
• Liyi Zhang - 浙江大学 - 模糊测试 - Monarch: A Fuzzing Framework for Distributed File Systems.
• Peng Cheng - 浙江大学 - 漏洞挖掘、机器学习

作者的思路

目前主流的基于覆盖率引导的模糊测试工具存在两个问题

• 默认选择覆盖新分支的种子进行模糊测试: 起初是生效的，但是随着时间推移覆盖新分支的种子愈发稀少并且间隔较远
• 丰富的变异算子对种子进行变异: 当测试进行到一定时间之后，解锁特定区域的代码块需要针对某个特定的字节进行变异，但是目前的变异算子无法满足。

针对这些问题目前的解决方案有

• 符号执行/约束求解: 通过识别与程序流相关的字节来改变输入用例中最相关的字节，但是仍然存在随着突变的进行对某些特定字节进行破坏的问题
• 机器学习过滤无关种子: 通过机器学习来过滤队列中无关的种子，但是其效果往往不好并且存在不可解释性的问题

所以作者为了解决以上问题提出了ATTFuzz

• ATTUZZ 根据覆盖未覆盖分支的概率及其数量来估计奖励
• ATTUZZ 训练了一个模型，该模型预测在给定种子的某些字节上的某些突变的情况下是否会覆盖某个“奖励”块

形式化定义

Definition 1. grey-box fuzzing problem

作者将灰盒模糊测试定义成为一个含有标签的转换系统$P$，其中$P=(B,init,V,\phi,GC,T)$

• $B$: 一组有限的基本块集合
• $init \in B$: $init$表示程序唯一的入口点
• $V$: 一组有限的变量集合
• $GC$: 是一组以$[g]f$形式存在的guarded command，其中$g$为guarded command而$f$通常为会更新变量$V$的函数，$f$通常表示为基本块
• $T$: 是一个转移函数，表示$B\times GC \rightarrow B$

$P$的具体执行是一个序列$\pi=<(v_0,b_0),gc_0,(v_1,b_1),gc_1,...,(v_k,b_k)，gc_k,...>$

• $v_i$：是$V$的估值
• $b_i$：$b_i \in B$
• $gc_i$：$gc_i = [g_i]f$，使得$(b_i,gc_i,b_{i+1}) \in T$，$v_i \models g_i$并且对于所有的$i$、$v_0 \models \phi$和$b_0=init$都有$v_{i+1}=f_i(v_i)$

作者使用$\Pi$来描述一组具体执行，当且仅当$b$在序列中时才可以说$\pi \in \Pi$覆盖了基本块$b$；当且仅当存在具体执行$\pi \in \Pi$覆盖了基本块$b$时，才可以说$\Pi$可以到达基本块$b$

Definition 2. Pre-dominate Block

作者也同样形式化定义了支配块(前驱块)的概念

给定一个基本块$b$，其支配块$D_b = {b'|b' \in B\ \& \ \exist\ g:(b',gb',b) \in T}$

直观上讲，基本块$b$的支配块$D_b$是可以一步转移到基本块$b$的基本块

Definition 3. Labeled discrete-time Markov chain(DTMC)

一个(标记的)离散时间马尔科夫链(DTMC)可表示为一个元组$M=(B,P_r,\mu)$

• $B$: $B$是$P$中所有基本块的集合
• $P_r$: $P_r = B \times B \rightarrow R^+$是标记转移概率函数，对于所有的$b \in B$有 $\sum_{b' \in B} P_r(b, b') = 1$
• $\mu$：$\mu$是初始概率分布使得$\sum_{b \in B}\mu_b=1$

如果对初始程序施加初始分布，就可以将程序抽象成为一个DTMC。程序中每一个基本块都可以成为DTMC中的一个状态，并且每两个基本块之间的边都与一个条件概率相关。

Definition4. Conditional Probability

令$\#(b_1,b_2)$表示为模糊测试过程中基本块$b_1$转移到基本块$b_2$的次数；$\#b_1$表示基本块$b_1$的执行次数；$n$是ICFG中基本块$b_1$的出度。

则基本块$b_1$转移到$b_2$的条件概率为 $P_r(b_1,b_2)=\frac{1+\#(b_1,b_2)}{\#b_1+n}$

作者在分子和分母上分别添加1和$n$，这样做的意义是即使$b_1$和$b_2$一次都没有执行过，在使用拉普拉斯变换时会将边缘转移概率估计为$\frac{1}{\#b_1+n}$而不是0，方便后续计算奖励

Definition 5. Reward of a basic block

定义基本块$b$的奖励为 $R_b$，其中$b \in B$；定义基本块$t$为基本块$b$一步可以到达的基本块，其中$t \in T$，有方程组

$R_b =\begin{cases} 1+\sum_{t \in T}\{P_r(b,t)\times R_t\},&if\ b \notin visited \\ \sum_{t \in T}\{p_r(b,t) \times R_t\}, &if b \in visited \end{cases}$

对于无法使用静态提取的间接调用，作者选择使用Fuzz的数据来动态补充ICFG

Definition 6. Convert seed file into a series of vector

作者将种子文件转化为变量$XD\times N=<v_1,v_2,...,v_n>,v_{m_{D\times1}},v_{p_{D\times1}}$

• $D$: $D$是字节嵌入的维度
• $N$: $N$是种子文件的最大长度

整体框架

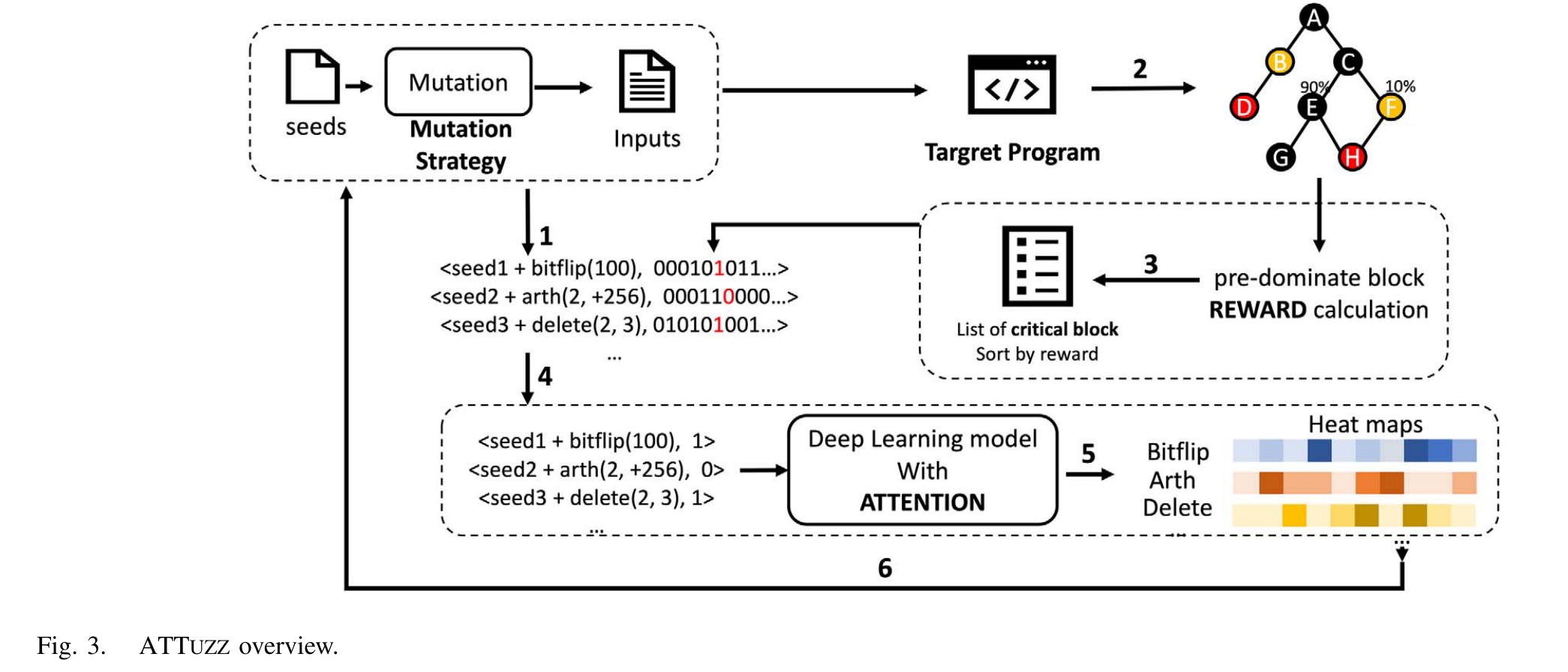
• 数据收集阶段：收集运行中的所使用的种子文件和突变算子，并且使用bitmap来收集覆盖率信息
• 奖励计算阶段
• 模型训练阶段
• 变异策略更新阶段

作者首先使用Fuzzer来收集和跟踪相关执行数据，主要包括执行过程中使用的种子文件、变异方法和每次执行所覆盖的范围，当模糊测试的覆盖增长陷入到瓶颈的时候激活ATTFuzz。

ATTFuzz的主要思想是采用深度学习的方法，预测种子和变异的组合是否可以覆盖到某些基本块。为了避免为每个基本块进行训练的数据不足和开销过大的问题，作者采用标记过后的离散时间马尔科夫链的形式构建程序的抽象。而后基于离散时间马尔科夫链寻找支配块，最后获取不同变异算子下种子的热图，最后通过训练注意力模型来指导选择更有价值的字节和更合适的变异算子进行变异直到克服当前瓶颈。

作者首先根据Definition 4和Definition 5来确定每个基本块的奖励，而后根据Definition 6来将种子文件抽象成为一个向量，而后根据目标的不同，使用不同的神经网络提取其特征(图像使用CNN，文本格式使用RNN)，然后使用注意力层来将注意力权重分配到每个特征中，最后根据加权特征使用全连接层进行分类。