🤔

FOX: Coverage-guided Fuzzing as Online Stochastic Control

作者

• Dongdong She - 香港大学 - 漏洞挖掘、模糊测试
• Adam Storek - 哥伦比亚大学 -
• Yuchong Xie - 香港大学 - 模糊测试
• Seoyoung Kweon - 哥伦比亚大学 -
• Prashast Srivastava - 哥伦比亚大学 - 模糊测试
• Suman Jana - 哥伦比亚大学 - 机器学习、漏洞检测、模糊测试

传统方案

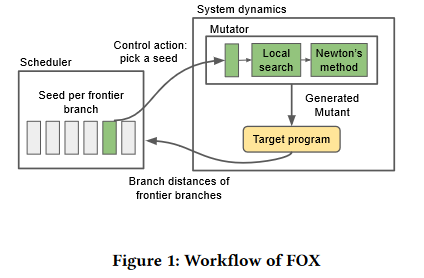
Scheduler: 传统覆盖率引导的模糊测试采用较为粗粒度的反馈(覆盖率反馈)选择进一步突变的样本，这种做法严重依赖先前产生的提升覆盖率的种子。随着模糊测试的进行，该调度方法往往会退化成为循环方法。

• 数据流引导的模糊测试: 先前有研究提出了反馈粒度更为精细的数据流引导的模糊测试，但是其往往会带来语料库爆炸的问题。

Mutator: 目前的Mutator和程序分支是无关的，其独立于分支逻辑执行随机突变，很显然存在盲目性。

• 污点分析: 虽然污点分析提供了分支定制的突变操作，但是其开销是无法接受的

总结来说，目前虽然Fuzzer = Scheduler + Mutator，但是当前的Fuzzer往往都是将其拆分为两个目标不同、数据交换很少的独立实体。

作者的方法论

覆盖率引导的模糊测试可以定义为一个在线优化问题，其目的是最大化目标程序的边缘覆盖率。

对于任意一个目标程序$P$，其输入样例长度为$M$；在每次模糊迭代$i$中，Fuzzer会从当前种子库$S_i$中选择一个种子$S_i[u_i]$，其中$u_i$为所选种子的索引。然后Fuzzer针对样本$S_i[u_i]$ 应用变异器$mut(\cdot)$ 生成新的输入$x$，而后程序将该变异输入执行并使用函数$cov(x,S_i)$来计算变异输入$x$和种子语料$S_i$实现的代码覆盖率提升。根据覆盖率结果Fuzzer会选择是否将输入样本$x$输入到语料库$S_i$中以生成语料库$S_{s+1}$，其目的可以总结为最大化$K$个阶段的代码覆盖率

可以形式化表示为: $Maximize\sum^K_{i=1}[cov(mut(S_i[u_i]),S_i)]$

Q1: 啥是在线优化问题?

在线优化问题是机器学习中的一个概念，在线学习代表了一系列机器学习算法，特点是每来一个样本就能训练，能够根据线上反馈数据，实时快速地进行模型调整，使得模型及时反映线上的变化，提高线上预测的准确率。相比之下，传统的批处理方式需要一次性收集所有数据，新数据到来时重新训练的代价也很大，因而更新周期较长，可扩展性不高。

如此以来就将模糊测试的覆盖率提升问题转化为一个最优控制问题，在最优控制问题中主要目标是在给定状态空间和控制空间的情况下找到最优控制策略。在目前的模糊测试方案中，状态空间可以定义为Fuzzer在每个阶段的状态，即当前的语料库$S_i$；而控制空间则对应于Fuzzer作出的选择，例如选择样本进行突变。

状态空间: Fuzzer 在任何给定阶段的所有可能的配置或者状态，简单来说就是第$i$阶段的语料库信息，用$S_i$来表示

控制空间: 包括所有可能影响系统行为的决策，简单来说就是在每个阶段选择哪一个种子，用种子语料$S_i$中的索引$u_i$表示

综上，由于Mutator的随机性质，Fuzzing过程是动态随机的，从形式上看，作者将动态步骤定义如下

$x \leftarrow mut(S_i[u_i]) \\ g_i = E[cov(x,S_i)] \\ S_{i+1} \leftarrow update(S_i, x, g_i)$

目标函数: 目标函数定义了系统的目标或预期结果，简单来说其目标是使得$K$个阶段的预期总覆盖最大，形式化表示为$Maximize\sum^K_{i=1}g_i$

制约因素: 系统需要满足的限制条件，简单来说就是总执行时间(每个阶段$t_i$的执行时间总和)不得超过Fuzzing处理活动的总时间预算$T$，形式化表示为$\sum^K_{i=1}t_i\le T$

从形式上讲，$cov(x,S_i)$可以建模为一个随机变量，该变量计算在阶段$i$中有多少个未被覆盖的条件分支被针对输入$x$的随机突变操作而翻转；故作者提出了一个指示函数$cov_b(x,S_i)$其结果是一个布尔值，如果在阶段$i$中条件分支$b$因为输入$x$而翻转则结果为$1$，反之为$0$。由此可以得出函数$cov$的数学期望为$g_i=\sum_{b\in B_i}E[cov_b(x,S_i)]$。

通过形式化某分支$b$翻转的概率为$Pr(b\ flips | mut(S_i[u_i]))$ 而 $x \leftarrow mut(S_i[u_i])$，所以可以结合上述公式推到出$g_i=\sum_{b\in B_i}Pr(b\ flips |mut(S_i[u_i]))$

而后为了能够估计$Pr(b\ flips |mut(S_i[u_i])$ 的值，作者引入了forontier node和horizon node的概念，作者将CFG视作$G=(N,E)$其中$N$为一组基本块，$E$表示这些基本块之间的控制流转换，在给定一个语料库$S$的前提下，可以根据代码覆盖率信息将$N$分类为一组未访问的节点$U$和一组访问过的节点$V$

形式化表示为$V=\{n|n\in N,S.cov(n)=1\} \\ U=\{n|n \in N , S.cov(n)=0\}$ ，其中$S.cov$表示在语料库中是否到达节点$n$；作者将forontier node定义为一组已访问的节点，并且其主导所有未访问的节点 [这不就是前驱结点么..] $F = \{v|(v,u)\in E,v\in V, u \in U\}$

Q2: 啥啥啥?

这里借鉴了文章Effective Seed Scheduling for Fuzzing with Graph Centrality Analysis的概念，但是没看懂

为了通过forontier node来反应覆盖率，作者只关注和条件跳转相关联的forontier node，即forontier branch。第$i$个阶段的forontier branch用$FB_i$来表示。假设第$i$个阶段的forontier node都涉及到对谓词$Q_b$的判断，谓词根据关系$f_b(x)\ R_b\ 0$来判断真假，其中$R_b$表示条件类型$(<,\le,>,\ge,=,\ne)$，x表示输入用例。翻转分支则表示找到一个输入$x'$，其是得$Q_b(f_b(x')) \ne Q_b(f_b(x))$，也就是说使条件的真假翻转。如果通过对Fuzzer的改造，使得Fuzzer在Fuzz过程中可以感知到每个forontier branch $b\in FB_i$的二元组$(Q_b(f_b(x),R_b))$，如此便可以定义分支距离算法